Versione italiana in fondo

As function of speed and safety distance

Recently it has been proposed a raise of the speed limit for some italian highways. This idea has been criticized, so I decided to make some calculations to understand whether it is really useful or not and to know the exact effects on the car flux a road can sustain.

The Italian Road Regulation

The law states (italian version) that every car has to keep a distance from the previous one such that they would never touch each other, no matter the circumstance. This law is pretty clear: the distance must be the sum of the space covered during the reaction time plus the space needed to completely stop. However, not everyone follow this rule: my own drive instructor told me to keep only the space ceovered during the response time, since it’s not enough to avoid the collision in only two situations: either there is a cross where you cannot see at all the other roads or a wall suddenly appears in the middle of the road, in front of the previous car. In a highway there aren’t crosses and wall probably will never appear, so the formula was given to me was ok.

In the real world, things go slightly different… most people don’t even know that the distance among cars should be adapted to actual speed, they keep a constant distance most of the time… it only depends on the road: urban road, 2 meters is ok, country road 8-10 meters (well, even less)m highway… about 15 meters. Just think about it.

The Formulas

When studying the problem, we can make some assumptions, to simplify thinkgs a bit. Let’s assume that all the cars drive at the maximum allowed speed, 130 km/h in almost every italian highway, fogetting about people that run slower than they could or faster than they should. Let’s also assume that the chosen distance (whatever it is) is always kept, so we ignore overtakings and every other event that could perturb the traffic.

Speaking about safety distance, these are the formulas involved (all the units are from SI: m/s for speeds, obtained with km/h divided by 3.6, and meters for distances):

where the first formula is everything many people know about, the second one represents the distance covered during the response time (1 second), the third one is proportional to the braking distance (proportional to the square of the speed: it’s related to kinetic energy) and the last one is the safety distance as defined in the italian regulation. Some formulas have constants, I chose those that have been taught to me, they should work well with today’s cars, they are experimental and not computed from theory.

The formula that gives the cars flux is the following:

The flux is represented by the greek letter Φ, the cars density with ρ, the car length with l and the distance among them with d (it must be substituted with one of the previous formulas).

Once we have the formulas, all we have to do is to plot graphs whith speed as independent variable and flux as dependent variable. In the following two graphs I show the results, in the first one I set l to 4 meters, while in the second one 10 meters (a truck instead of a car). Axis scales are kept constant, in order to allow easy comparisons. The ordinates axis represents how many cars transit per second (imagine to stop on a side of the road and to count how many cars every second you see). All the graphs have been plotted with MathPad, a free utility for Mac OS. The source code used is available here:

Xmin=0
Xmax=50
Xdiv=5
Ymin=0
Ymax=1.25
Ydiv=0.25
~
plot X/(10+20)
plot X/(10+X)
plot X/(10+0.13*X^2)
plot X/(10+X+0.13*X^2)
~
plot X/(4+20)
plot X/(4+X)
plot X/(4+0.13*X^2)
plot X/(4+X+0.13*X^2)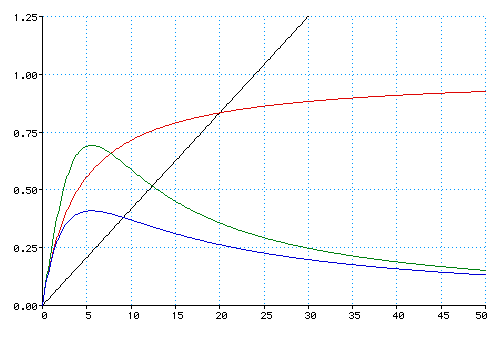

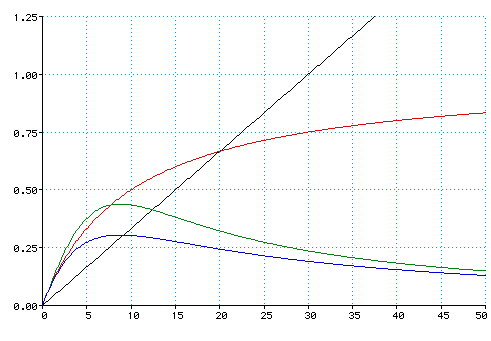
The color shows how the distance has been calculated: black means constant distance (20 meters should be realistic), red means distance proportional to the speed, green means proportional to braking distance, blue is the distance according to the official regulation. The X axis ranges from 0 to 50 m/s, in other words from 0 km/h to 180 km/h. The Y axis has been limited to 1.25 cars/second, to show with more details the useful curves.

Final Results

It’s pretty clear that a generalized speed limit increase cannot give an overall benefit (if everyone followed the rules), however, if applied only to highways without traffic jams, it can help to reduce travel time (time = space / speed).

I think the idea of raising the speed limit from 130 km/h to 150 km/h (41.7 m/s) in selected stretchs of road is a good choice to reduce travel time, while in city streets the limit must not be touched, since a lower speed limit allows for greater fluxes, much more useful (the maximum flux is obtained with a speed equal to about 5,5 m/s, or 19,8 km/h if you prefer).

A thought about safety distances: it’s interesting to think what a great benefit could an integrated electronic traffic control could give… with much shorter response times we could raise a lot the speed limit and keep a constant distance between vehicles to achieve the fluxes of the black line in the graphs, about 10 times greater than the blue line at 50 m/s!

If you’d like to have more details and info’s, feel free to contact me by electronic mail.

First revision: March 5th, 2006.

Calcolo del flusso di auto in una strada

Al variare di velocità e distanza di sicurezza, in base alla legislazione italiana

Di recente è stato proposto, in Parlamento, l’aumento del limite massimo di velocità per alcuni tratti delle autostrade italiane. Per capire se ciò possa davvero portare benefici in termini di snellimento del traffico e per smentire o confermare alcune critiche, ho deciso di effettuare i calcoli rigorosi partendo da varie ipotesi di lavoro.

Il codice della strada

Il codice della strada stabilisce che “Durante la marcia i veicoli devono tenere, rispetto al veicolo che precede, una distanza di sicurezza tale che sia garantito in ogni caso l’arresto tempestivo e siano evitate collisioni con i veicoli che precedono.”. Questa definizione lascia pochi dubbi in merito: la distanza deve essere quella di frenata più quella percorsa nel tempo di reazione del guidatore. Fin qui la teoria, ma nella pratica è diverso: ricordo chiaramente che il mio istruttore di guida mi indicò, come distanza di sicurezza, la sola distanza percorsa nel tempo di reazione! il motivo, beninteso, era semplice e più che logico: a meno che non ci si trovi in un incrocio senza visuale ed a meno che non si supponga possibile la comparsa di muri verticali in mezzo alla strada, la formula è perfettamente sufficiente ad impedire il contatto. Poiché in autostrada incroci non ve ne sono e muri dal nulla non compaiono, la sua formula era ok.

Fino a qui i motivi teorici per l’una o l’altra scelta… passiamo alla realtà: la maggior parte della gente non si sogna nemmeno di variare la distanza di sicurezza in base alla velocità, la maggior parte del tempo mantiene una distanza dal veicolo che li precede quasi costante, scegliendola in base alla strada! strada urbana? 2 metri è la norma, strada extraurbana 8-10 metri (beh, spesso meno) e autostrada una quindicina. Fateci caso…

I calcoli

Nella valutazione del problema, per semplificare la trattazione, consideriamo alcune ipotesi. La prima è che tutte le macchine si muovano alla massima velocità consentita dalla legge, nel nostro caso a 130 km/h (limite di legge per la maggior parte delle autostrade), trascuriamo quindi tutti coloro che vanno più lenti e tutti coloro che superano i limiti di legge. La seconda ipotesi adottata è che sia sempre mantenuta la distanza di sicurezza scelta (giusta o sbagliata che sia) fra due automobili. Questo esclude quindi sorpassi e casualità varie.

Le formule coinvolte nel calcolo della distanza di sicurezza sono le seguenti (tutte le unità di misura sono quelle del SI: le velocità sono indicate in m/s, le si ottiene dividendo le velocità in km/h per 3,6, le distanza in metri):

dove la prima è quella usata da molte persone, la seconda quella percorsa nel tempo di reazione (1 secondo), la terza quella proporzionale allo spazio di frenata (che aumenta col quadrato della velocità, essendo connessa all’energia cinetica del mezzo), l’ultima quella secondo la normativa. Nel calcolo delo spazio di frenata ho usato la costante che mi fu insegnata, valida per i veicoli odierni e ottenuta mediante misure sperimentali degli spazi di frenata.

La formula che permette di ottenere il flusso di auto in una specifica strada è la seguente:

Il flusso è indicato con la lettera Φ, la densità di auto con ρ, la lunghezza di ogni auto con l e la distanza tra esse con d (che va sostituita con una delle formule sopra elencate).

Una volta ottenute le formule, è sufficiente tracciare un grafico con la velocità come unica variabile indipendente, mentre il flusso di auto diventa la viariabile dipendente. Nelle due immagini seguenti si vede il risultato, nel primo grafico la lunghezza delle auto è stata fissata a 4 metri, nel secondo 10 metri (prossima a quella di autorimorchi). Le scale degli assi sono state uniformate, per permettere il confronto. L’asse delle ordinate indica il numero di auto che passano al secondo, come se ci si mettesse in una piazzola e si contassero quelle che passano davanti ai propri occhi. Per tracciare i grafici è stato utilizzato MathPad, un’applicazione gratuita per Mac OS. Il sorgente utilizzato è disponibile qui:

Xmin=0
Xmax=50
Xdiv=5
Ymin=0
Ymax=1.25
Ydiv=0.25
~
plot X/(10+20)
plot X/(10+X)
plot X/(10+0.13*X^2)
plot X/(10+X+0.13*X^2)
~
plot X/(4+20)
plot X/(4+X)
plot X/(4+0.13*X^2)
plot X/(4+X+0.13*X^2)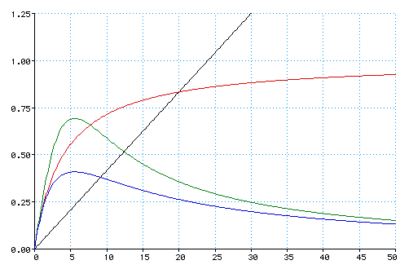

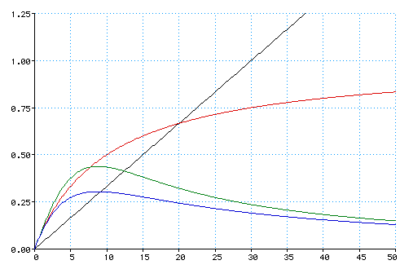
Il colore delle linee rappresenta la formula utilizzata per il calcolo della distanza di sicurezza: nero per distanza costante (20 metri per stare abbondanti), rosso per la distanza proporzionale alla velocità del mezzo, verde la distanza proporzionale allo spazio di frenata, blu la distanza calcolata secondo la normativa. I calcoli sono stati effettuati per la velocità da 0 m/s fino a 50 m/s, che corrispondono a 180 km/h, ed i valori di flusso sono stati troncati a 1,25 auto/secondo, per mostrare meglio l’andamento delle curve più utili.

Conclusione

Non vi sono dubbi che l’aumento del limite di velocità non possa portare vantaggi se si ragiona in termini di scorrevolezza delle strade e si suppone di rispettare il codice della strada, però, applicato solo a tratti già scorrevoli e mai intasati dal traffico, il vantaggio esiste: i tempi di percorrenza dei singoli guidatori si riducono (tempo = spazio / velocità).

Nel complesso, quindi, ritengo che la scelta di innalzare il limite a 150 km/h (41,7 m/s nel grafico) nei tratti già sgomberi da traffico sia la scelta giusta, mentre è importante evitare assolutamente di innalzare tale limite nei centri abitati, dove notoriamente il problema non è il tempo di percorrenza ma, al contrario, l’intasamento delle strade (la velocità che permette il flusso massimo di auto è intorno a 5,5 m/s, corrispondenti a 19,8 km/h).

In merito ai vari metodi di calcolo della distanza di sicurezza, è interessante notare quale enorme vantaggio si potrebbe avere se si affidasse interamente il controllo del traffico a sistemi elettronici automatici, caratterizzati da tempi di risposta decisamente minori da quelli umani: si potrebbe innalzare il limite senza problemi e, in aggiunta, l’andamento del flusso di auto seguirebbe la linea nera (distanza costante fra autoveicoli), che a 50 m/s di velocità permette flussi più di 10 volte superiori a quelli ottenibili con la normativa vigente!

Per ulteriori chiarimenti o commenti, contattatemi per via elettronica.

Prima stesura: 5 Marzo 2006.